Siméon Denis Poisson
From Wikipedia, the free encyclopedia
 Siméon Denis Poisson | |
| Born | June 21, 1781 Pithiviers, France |
|---|---|
| Died | April 25, 1840 |
| Nationality | |
| Alma mater | École Polytechnique |
| Academic advisor | Joseph Louis Lagrange |
| Notable students | Michel Chasles |
| Religion | atheism |
Siméon-Denis Poisson (June 21, 1781 – April 25, 1840), was a French mathematician, geometer, and physicist. The name is pronounced [simeõ d̪əni pwasõ] in French.
Contents[hide] |
[edit] Biography
Poisson was born in Pithiviers.
In 1798, he entered the École Polytechnique in Paris as first in his year,and immediately began to attract the notice of the professors of the school, who left him free to follow the studies of his predilection. In 1800, less than two years after his entry, he published two memoirs, one on Étienne Bézout's method of elimination, the other on the number of integrals of an equation of finite differences. The latter of these memoirs was examined by Sylvestre-François Lacroix and Adrien-Marie Legendre, who recommended that it should be published in the Recueil des savants étrangers, an unparalleled honour for a youth of eighteen. This success at once procured for Poisson an entry into scientific circles. Joseph Louis Lagrange, whose lectures on the theory of functions he attended at the École Polytechnique, early recognized his talent, and became his friend (the Mathematics Genealogy Project lists Lagrange as his advisor, but this may be an approximation); while Pierre-Simon Laplace, in whose footsteps Poisson followed, regarded him almost as his son. The rest of his career, till his death in Sceaux near Paris, was almost entirely occupied in the composition and publication of his many works, and in discharging the duties of the numerous educational offices to which he was successively appointed.
Immediately after finishing his course at the École Polytechnique he was appointed repetiteur there, an office which he had discharged as an amateur while still a pupil in the school; for it had been the custom of his comrades often to resort to his room after an unusually difficult lecture to hear him repeat and explain it. He was made deputy professor (professeur suppléant) in 1802, and, in 1806 full professor in succession to Jean Baptiste Joseph Fourier, whom Napoleon had sent to Grenoble. In 1808 he became astronomer to the Bureau des Longitudes; and when the Faculté des Sciences was instituted in 1809 he was appointed professor of rational mechanics (professeur de mécanique rationelle). He further became member of the Institute in 1812, examiner at the military school (École Militaire) at Saint-Cyr in 1815, leaving examiner at the École Polytechnique in 1816, councillor of the university in 1820, and geometer to the Bureau des Longitudes in succession to P. S. Laplace in 1827.
In 1817, he married Nancy de Bardi and with her he had [several?] children. His father, whose early experiences led him to hate aristocrats, bred him in the stern creed of the first republic. Throughout the Revolution, the Empire and the following restoration, Poisson was not interested in politics, concentrating on Mathematics. He was appointed to the dignity of baron in 1821; but he neither took out the diploma or used the title. The revolution of July 1830 threatened him with the loss of all his honours; but this disgrace to the government of Louis-Philippe was adroitly averted by François Jean Dominique Arago, who, while his "revocation" was being plotted by the council of ministers, procured him an invitation to dine at the Palais Royal, where he was openly and effusively received by the citizen king, who "remembered" him. After this, of course, his degradation was impossible, and seven years later he was made a peer of France, not for political reasons, but as a representative of French science.
Like many scientists of his time, he was an atheist.
As a teacher of mathematics Poisson is said to have been more than ordinarily successful, as might have been expected from his early promise as a repetiteur at the École Polytechnique. As a scientific worker his activity has rarely if ever been equalled. Notwithstanding his many official duties, he found time to publish more than three hundred works, several of them extensive treatises, and many of them memoirs dealing with the most abstruse branches of pure, applied mathematics, mathematical physics and rational mechanics.
A list of Poisson's works, drawn up by himself, is given at the end of Arago's biography. All that is possible is a brief mention of the more important. It was in the application of mathematics to physical subjects that his greatest services to science were performed. Perhaps the most original, and certainly the most permanent in their influence, were his memoirs on the theory of electricity and magnetism, which virtually created a new branch of mathematical physics.
Next (perhaps in the opinion of some first) in importance stand the memoirs on celestial mechanics, in which he proved himself a worthy successor to P.-S. Laplace. The most important of these are his memoirs Sur les inégalités séculaires des moyens mouvements des planètes, Sur la variation des constantes arbitraires dans les questions de mécanique, both published in the Journal of the École Polytechnique (1809); Sur la libration de la lune, in Connaiss. des temps (1821), etc.; and Sur le mouvement de la terre autour de son centre de gravité, in Mém. d. l'acad. (1827), etc. In the first of these memoirs Poisson discusses the famous question of the stability of the planetary orbits, which had already been settled by Lagrange to the first degree of approximation for the disturbing forces. Poisson showed that the result could be extended to a second approximation, and thus made an important advance in the planetary theory. The memoir is remarkable inasmuch as it roused Lagrange, after an interval of inactivity, to compose in his old age one of the greatest of his memoirs, entitled Sur la théorie des variations des éléments des planètes, et en particulier des variations des grands axes de leurs orbites. So highly did he think of Poisson's memoir that he made a copy of it with his own hand, which was found among his papers after his death. Poisson made important contributions to the theory of attraction.
[edit] Contributions
Poisson's well-known correction of Laplace's partial differential equation of the second degree for the potential:
today named after him the Poisson's equation or the potential theory equation, was first published in the Bulletin de in société philomatique (1813). If a function of a given point ρ = 0, we get Laplace's equation:
In 1812 Poisson discovered that Laplace's equation is valid only outside of a solid. A rigorous proof for masses with variable density was first given by Carl Friedrich Gauss in 1839. Both equations have their equivalents in vector algebra. The study of scalar field φ from a given divergence ρ(x, y, z) of its gradient leads to Poisson's equation in 3-dimensional space:
For instance Poisson's equation for surface electrical potential Ψ, which shows its dependence from the density of electrical charge ρe in particular place:
The distribution of a charge in a fluid is unknown and we have to use Poisson-Boltzmann equation:
which in most cases cannot be solved analytically but just for special cases. In polar coordinates the Poisson-Boltzmann equation is:
which also cannot be solved analytically. If a field φ is not a scalar, the Poisson equation is valid, as can be for example in 4-dimensional Minkowski space:
If ρ(x, y, z) is a continuous function and if for r→∞ (or if a point 'moves' to infinity) a function φ goes to 0 fast enough, a solution of Poisson's equation is the Newtonian potential of a function ρ(x, y, z):
where r is a distance between the element with the volume dv and point M.
Integration runs over the whole space. The Poisson's integral in solving the Green's function for the Dirichlet problem of the Laplace's equation, if circle is investigated domain:
where
φ(χ) is prescribed function on a circular line, which defines bounding conditions of requested function φ of Laplace's equation.
In the same manner we define the Green's function for the Dirichlet problem of the Laplace's equation ∇2 φ = 0 in space, if we look to the investigated domain of a sphere with a radius R. This time the Green's function is:
where
is a distance of a point (ξ, η, ζ) from the center of a sphere
r a distance between points (x, y, z)
(ξ, η, ζ), r1 is a distance between the point (x, y, z) and the point (Rξ/ρ, Rη/ρ, Rζ/ρ), symmetrical to the point (ξ, η, ζ)
The Poisson's integral now has a form:
Poisson's two most important memoirs on the subject are Sur l'attraction des sphéroides (Connaiss. ft. temps, 1829), and Sur l'attraction d'un ellipsoide homogène (Mim. ft. l'acad., 1835). In concluding our selection from his physical memoirs we may mention his memoir on the theory of waves (Mém. ft. l'acad., 1825).
In pure mathematics, his most important works were his series of memoirs on definite integrals, and his discussion of Fourier series, which paved the way for the classical researches of Peter Gustav Lejeune Dirichlet and Bernhard Riemann on the same subject; these are to be found in the Journal of the École Polytechnique from 1813 to 1823, and in the Memoirs de l'académie for 1823. He also studied Fourier integrals. In addition we may also mention his essay on the calculus of variations (Mem. de l'acad., 1833), and his memoirs on the probability of the mean results of observations (Connaiss. d. temps, 1827, &c). The Poisson distribution in probability theory is named after him.
In his Traité de mécanique (2 vols. 8vo, 1811 arid 1833), which was written in Laplace and Lagrange style and was long a standard work he showed many new grips such as an explicit usage of impulsive coordinates:
which has influenced on the work of William Rowan Hamilton and Carl Gustav Jakob Jacobi.
Besides his many memoirs Poisson published a number of treatises, most of which were intended to form part of a great work on mathematical physics, which he did not live to complete. Among these may be mentioned
- Nouvelle théorie de l'action capillaire (4to, 1831);
- Théorie mathématique de la chaleur (4to, 1835);
- Supplement to the same (4to, 1837);
- Recherches sur la probabilité des jugements en matières criminelles et matière civile (4to, 1837), all published at Paris.
In 1815 Poisson carried out integrations along paths in the complex plane. In 1831 he independently of Claude-Louis Navier derived the Navier-Stokes equations.
[edit] See also
[edit] External links
- O'Connor, John J; Edmund F. Robertson "Siméon Denis Poisson". MacTutor History of Mathematics archive.
- Siméon Denis Poisson at the Mathematics Genealogy Project
[edit] References
- This article incorporates text from the Encyclopædia Britannica Eleventh Edition, a publication now in the public domain.
| Awards | ||
|---|---|---|
| Preceded by George Biddell Airy | Copley Medal 1832 jointly with Michael Faraday | Succeeded by Giovanni Antonio Amedeo Plana |



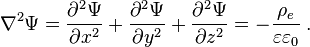
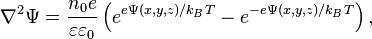





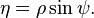
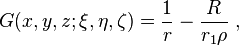
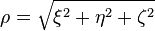




No comments:
Post a Comment